繰り上がりのある足し算は2STEP！

数字カードを数えさせよう！

子どもの手元に【8】のカード1枚、すこし離れたところに【1】のカード３枚を置いてください。
※正確には【8】（間をあける）【1】【1】【1】（←横に並べてください）



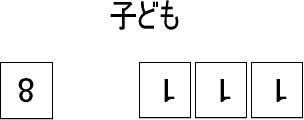
そして、「何枚カードがあるか数えてみて」といってください。
子どもが、つぎのように「９」「１０」「１１」と数えられればOKです。



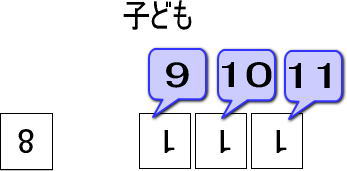
うまく数えられない場合は、【8】のカードの近くに【1】のカードを８枚置いて、「【8】と【1】のカード８枚は同じだよね。何枚カードあるか数えてみて」といってください。



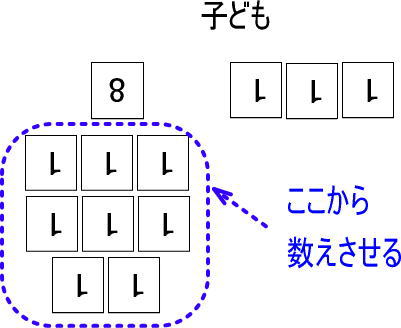
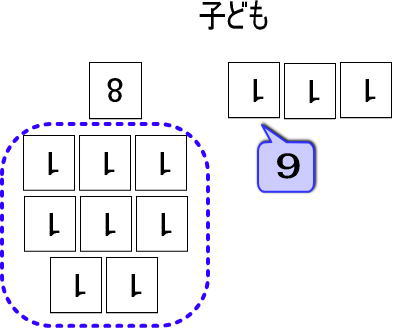
「１」「２」……。と数えていって「８」「９」と言ったところで、「ストップ！」
そして、【1】のカードの１枚目が、数えれば「９」であることを何度も確認してあげてください。
※「【8】のカードは【1】のカード８枚だから、つぎに数えるときは９だよね」などと言う感じです。

数字カードを数える反復練習しよう！

子どもの手元に【9】のカード１枚、すこし離れたところに【1】のカード３枚を置いてください。
※正確には【9】（間をあける）【1】【1】【1】（←横に並べてください）

そして、【9】のカードに一番ちかい【1】のカードを指さして「これは何番目？（※）」と聞いてください。



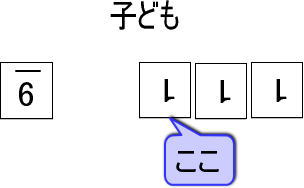
「１０」と答える子どももいますが、なかなか難しいものです。

もしわからない場合は、【9】のカードの近くに【1】のカードを９枚置いて、「【9】と【1】のカード９枚は同じだよね。カードを数えてみて」といってください。



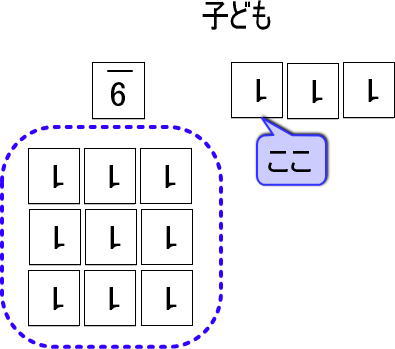
答えが「１０」だとわかると思います。

これを繰り返します。

子どもによっては、なかなかできないと思いますが、前に書いた通り、子どもは「パターン」で理解する傾向があります。
繰り返し、何度も同じような問題を解かせることで身につくので「これ、何度やるんだよ…」とならずに、繰り返してあげましょう。
ちなみに、繰り返し説明していると「またかよ…」「これで何度目だよ…」と思うときもあります。イラッとしたら、勉強はやめて気分転換するといいでしょう。

＜練習＞
・子どもの手元に５〜９のカードを１枚置いてください。
・間をあけて、１のカードを３枚ほど置いてください。
・１のカードの１枚目は何枚目か聞いてください。
・すんなりできる子どももいます。その場合は、５〜９のカードで練習したあと、１０以降のカードを置いて練習させても構いませんが、無理をする必要はありません。

「●＋３」の足し算を練習しよう！

子どもの手元に【8】【3】のカードを置いてください。
そして、「８＋３はいくつ？」と聞いてみてください。



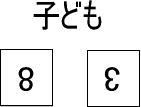
答えが１０を超えるので指で数えるのは難しいですし（それでも指で数える子どももいると思いますが）、いままでの方法だと、「【8】は【1】のカードが８枚、【3】は【1】のカードが３枚。これらをあわせるわけだから、１枚、２枚、３枚…」と数えていかなければならず、たいへんです。

そこで、子どもの手元の【3】のカードの左（子どもから見て左）に【1】のカードを３枚、横に並べてください。そして、「左にある【1】のカードは何枚目だったっけ？」と聞いてみてください。



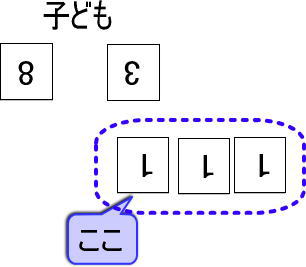
先ほどのことができていれば「９枚目」と答えられると思います（答えられないのなら、先ほどのことをふたたび繰り返してください）。

あとは、【3】のカードの隣の【1】のカードを指さしながら、「９枚目、１０枚目、１１枚目」と数えます。
すると、答えは「１１」だと、子どもは気がつきます。

もしわからなければ、何度も繰り返してください。
そのうち、法則性に気がつきますから。

＜ヒント＞
子どもがなかなか答えないと、イライラして、解法を言ってしまうかたもいると思います。
気持ちはよくわかります。
しかし、そのようにすると、解きかたを丸暗記してしまい、考えない子どもになってしまいます。
かといって、ずっと考えさせても、子どもの口から永遠に正答はでてきません。
「２分間、考えさせても答えがでない　→　ヒントをいう　→　さらに２分間経っても答えがわからない　→　解法を教える」などのようにして、できるだけ子どもに考えさせる時間をつくってあげましょう。

つぎは、紙につぎのタイプのたし算を書いて計算をさせてみましょう。

・「●＋２」のタイプのたし算
（例）「８＋２」「９＋２」「１０＋２」「２４＋２」など

・「●＋４」のタイプのたし算
（例）「８＋４」「９＋４」「２２＋４」など

・できるならば「●＋５」のタイプのたし算。ただし、これは別の計算法もあるので無理をする必要はありません。

数をかぞえる延長線上で、足し算の練習をさせよう！

あとは反復練習です。
つぎの練習問題を解かせましょう。
※この際、ランダムに出題してください。

・９＋２＝
・９＋３＝
・９＋４＝

・８＋２＝
・８＋３＝
・８＋４＝

・７＋２＝
・７＋３＝
・７＋４＝

・６＋２＝
・６＋３＝
・６＋４＝

これができれば、いままでの「３＋２」のような、かんたんな、たし算も混ぜて、計算させましょう。

「１０＋●」「●＋１０」の計算に慣れさせよう！

「１０＋３＝」と紙に書いて、子どもに答えがいくつになるか考えさせてください。

答えられないなら、数字カードを取り出して、子どもの手元に【1】のカードを１０枚、すこし間をあけて【1】のカードを３枚置いてください。



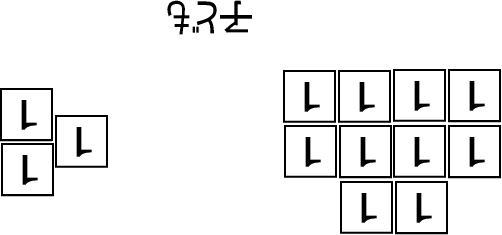
そして、「１０枚あるよね。数えるとここまでで１０枚だよね。で、３枚のほうを数えていくんだよね。１０のつぎは１１だから、１１、１２、１３と数えられるよね。だから、答えは１３」のように教えて、「１０＋３＝１３」と紙に書いてください。

その式の真下に「１０＋４」と書いてください。
で、子どもに答えがいくつになるのか考えさせてください。
※もしわからないようであれば、先ほどと同じようにカードを使って教えてください。

子どもが正解を答えたら「１０＋４＝１４」と書いてください。
その式の下に「１０＋５＝」と書いて、子どもに答えがいくつになるのか考えさせてください。

これを繰り返していきます。
「１０＋３＝」からはじめて、「１０＋９＝」あたりで、子どもは法則に気がつくと思います。
子どもが法則に気がついたな、と思ったら、「１０＋１０＝」の答えがいくつになるのか考えさせてください。

ここで、ひっかかる子どもには、紙に「１０＋９＝」を書いて、いくつか答えさせてください。
「１９」と答えたら、その下に「１０＋１０＝」を書いて「１９から１増えただけだよね？」と言ってください。
正解に気がつくと思います。

もしわからないようでしたら、子どもの手元に【1】のカードを９枚、すこし間をあけて【1】のカードを１０枚置いてください。
そして、「これは、たし算にすると、どうなる？」と聞いてください。



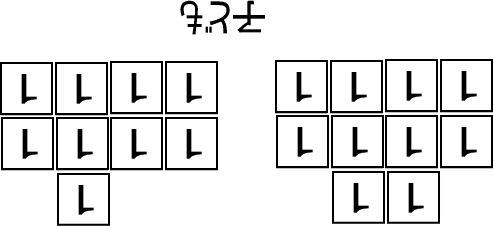
「１０＋９」もしくは「９＋１０」と言うと思います。そして、答えは「１９」だとわかると思います。

そこに【1】のカードを１枚加えてください。「これは、『１０＋１０』だよね？　いくつになる？」と聞くと「２０」と答えると思います。
※わからないようでしたら、復習してください。

＜目標＞「１０＋●」「●＋１０」がわかる。
※●は１〜１０までの整数

＜練習＞
つぎのたし算を計算させてください。
※ランダムに出題する、一項目と二項目を入れかえる（例：「１０＋１」→「１＋１０」）も練習させてください。

・１０＋１
・１０＋２
・１０＋３
・１０＋４
・１０＋５
・１０＋６
・１０＋７
・１０＋８
・１０＋９
・１０＋１０

片方を「１０」にして、もう片方から「借りる」

紙に「８＋７＝」と書いて、子どもに見せてください。
そして、「８を１０にするには、どうすればいい？」と聞いて、８のうえに１０と書いてください。



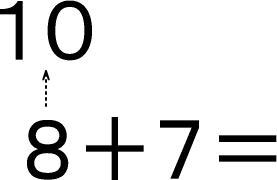
今までのことがしっかりできていれば、「２」と答えると思います。
できない場合は、つぎのいずれで教えてください。

＜考えかた１＞
８のつぎは９です。そのつぎは１０なので、「２」進めますね。すなわち２を足します。STEP1の方法ですね。

＜考えかた２＞
１０と８の差に着目します。「１０−８」で「２」です。前のページで学習しましたね。

＜【推奨】考えかた３＞
１０の補数を暗記していれば、１０の補数のうち、片側が８なので、もう一方が「２」だとわかります。
しっかり練習していれば自然に覚えていると思いますが、もし子どもが１０の補数を覚えていないのならば、この機会に１０の補数を暗記させておきましょう。

そして、「８に２を足して、１０にしたんだよね。その２はどこから持ってきた？」と聞いてください。
わからないと思うので、「こっちの７から借りてきたんだよ」と言ってください。
そして、「７から２を借りるといくつになる？」と聞いてください。

ひき算ですね。
具体的には「７から２を借りるってことは、２なくす、２引くってこと」と教えてください。
すると「５」と答えると思いますが、正解すればつぎのように書きこんでください。



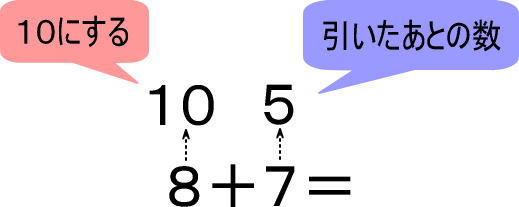
あとは「『１０＋５』は『１５』だよね。こうやって、８＋７は計算すればいいんだ」と教えてください。
まだわかっていないと思うので、つぎは、親と一緒に、つぎの練習問題を解かせましょう。
なお、このとき、式のうえに、かならず「１０」と「引いたあとの数」を書かせるようにしてください。
特に幼稚園児くらいだと、まだ意味をいまいち理解しておらず、これを書かないと何をしているのかわからなくなることがあるためです。
※大きいほうの数を１０にしますが、この段階ではまだ教えなくても構いません。

＜練習問題＞
つぎの計算をしてください。
※すこしでもわからないようならば、「まず、１０にする。１０を書いて」「１０にするためにいくつ借りる？借りたら（引いたら）いくつになる？書いて」と言ってください。
※子どもの状況によっては、練習問題を増やしてください。

・９＋６
・８＋５
・７＋６

繰り上がりのある足し算に慣れよう！

紙に「６＋９＝」と書いて、計算させてください。

子どもは６の上に「１０」を書くと思います。
そして、子どもが「１５」と答えたあと、つぎのような会話をしてください。

（親）６を１０にするにはいくつ必要？
（子ども）４
（親）だから「９−５」を計算するわけだよね。
（子ども）うん
（親）今度は９の上に１０を書いてみて。９を１０にするにはいくつ必要？
（子ども）１
（親）６から１を借りるわけだよね。計算式でいうと？
（子ども）「５−１」
（親）６の上に１０を書いたとき、（９を指さして）ここから４を引いたじゃん。でも、９の上に１０を書くと、（６を指さして）ここから１を引くだけでいいよね。どちらが計算は楽？
（親）だから、大きいほうの数字の上に１０を書くんだよ。

これを理解できれば御の字。
理解できない場合は「大きいほうの数字のうえに１０を書くのが決まり」とでもいって覚えさせてください。
あとは、練習問題を解かせていきましょう。

＜練習＞ ・６＋４＝
・６＋５＝
・６＋６＝
・６＋７＝
・６＋８＝
・６＋９＝

・７＋３＝
・７＋４＝
・７＋５＝
・７＋６＝
・７＋７＝
・７＋８＝
・７＋９＝

・８＋２＝
・８＋３＝
・８＋４＝
・８＋５＝
・８＋６＝
・８＋７＝
・８＋８＝
・８＋９＝

・９＋１＝
・９＋２＝
・９＋３＝
・９＋４＝
・９＋５＝
・９＋６＝
・９＋７＝
・９＋８＝
・９＋９＝