中学受験の算数をこうやって教えています!
中学受験の算数でどのような勉強をするのかを知っているかたは、「(当時)年長が予習シリーズ4年?」「小3が偏差値56の入試問題の過去問で合格点? 嘘だろ?」と思っていることでしょう。
算数の勉強会をしていたころ、うちの子どもたちが、実際に予習シリーズで問題を解いているのを見ていただいたこともあります。
で、「本当に解けている!」と思ったかたは、「どのようにすれば低年齢でも受験算数ができるようになるの?」と思うかもしれないな、と思ったので、サンプルを書いてみました。
ちなみに、実際は、もっと、ていねいに解説しています。すべて書くと大変なので割愛していて、わかりにくい箇所もあるかもしれません。あらかじめご了承ください。
1−1.算数は「つながり」を意識させている!
1−2.公式は極力覚えさせない(つながりだけで解決!)
1−3.算数はイメージ!
1−4.子どもの理解度に応じた教えかたを選択!
2.算数の教えかたのサンプル!
2−1.かけ算は「ハンコ」をイメージさせる
2−2.かけ算のイメージがあれば、面積図もかんたん!
2−3.割り算は分割法からイメージさせる
2−4.かけ算と割り算の関係性から、わり算の計算方法をイメージさせる
2−5.たった2つのイメージで、逆数ができる!(小4の受験算数)
2−6.割り算の余りの処理(小4の受験算数)
2−7.周期算(小4の受験算数)
3.「●番目と▲番目の真ん中は何番目?」
3−1.基数と序数を意識させる計算方法
3−1−1.真ん中とは?
3−1−2.1番目から●番目の真ん中
3−1−3.●番目から▲番目の真ん中(流れを説明)
3−1−4.●番目から▲番目の真ん中(計算方法を説明)
3−2.実践的な計算方法
3−2−1.真ん中は何個目?
3−2−2.真ん中まで同じ個数を利用
4.困ったプロも多い!
算数は「つながり」と「イメージ」。そして公式は極力覚えさせない
「受験算数は思考力を奪う!」
このように主張されるかたたちもいるようです。
このようなかたたちは、きっと腕の悪い塾講師に教わったのでしょう。
・ワケもわからないまま公式を丸暗記させられる!
・大量の問題演習をさせられる!
・とりあえず解けるようになったけど…
このように教わると、確かに思考力は奪われていくと思います。
苦痛で算数が嫌いになるかもしれません。
しかし!
わたしの教えかただと、思考力が奪われるどころか、ぐんぐんのびていきます。
いや、
現在も、どんどん、のびているというほうが正確ですね。
では、腕の悪い塾講師と、何がちがうのでしょうか。
算数は「つながり」を意識させている!
算数は、それぞれの単元が、つながっています。
たとえば、つぎのような「つながり」があります。
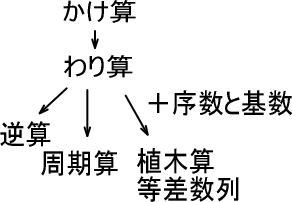
このつながりを意識して教えています。
だから、子どもの頭のなかで、それぞれの項目がつながっていって、どんどん思考力があがっているのだと思います。
公式は極力覚えさせない(つながりだけで解決!)
腕が悪い塾講師だと、つぎのように教えると思います。
・植木算:「このパターンは+1だったよね!」
・等差数列:「和の公式を覚えている? 公式を使えば、一発で解けるよね!」
→1.公式を覚えさせる、2.植木算と等差数列が、まるで別物のように解説!
わたしから言わせれば植木算も等差数列も同じですし、公式なんて覚えなくてもできるようになります。何より、植木算や等差数列を通して、算数を深く理解させることができるのに、その絶好の機会を放棄していると思います(だから、思考力を育てられない!)。
ちなみに、最終的には、はやく解けるようにするために公式を覚えさせます。はじめての単元で、公式から教えるのは愚の骨頂だといいたいだけです。
算数はイメージ!
算数はイメージだと思っています。
当時小1の息子が描いた、わり算(※)のイメージです。
こういうイメージを使って、教えています。
※後述していますが、やや強引に教えたときの包括法です。
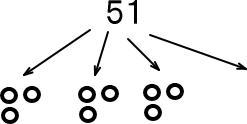
子どもの理解度に応じた教えかたを選択!
「年長の娘は算数の思考力がまだ育っていないから、この教えかた」
「小2の息子の算数の思考力は、小5の偏差値50くらいの子くらいだな。だから、この教えかた」
このように子どもの理解力によって、教えかたを変えています。
もちろん、市販の参考書にあるような「そうやって教えると、偏差値50までしかあがらないじゃん…」のような教えかたはしません。
算数の思考力がない子どもにも、先につながる教えかたで、教えています。
詳しくは「●番目から▲番目の真ん中は何番目」のところにあります。
算数の教えかたのサンプル!
かけ算、わり算、図形(面積)、周期算で、かんたんに説明してみます。
実際に子どもたちに教えたときは、もっと、ていねいに教えています。どのようなものなのかを、わかっていただくために、ざっと書いているので、わかりにくい箇所もありますので、あらかじめご了承ください。
かけ算は「ハンコ」をイメージさせる
●が3つあるハンコがあったとするね。

これを、ポン、ポン…と4回と押していったら、どうなると思う?
つぎのようになるよね。

これを式にしたら「3(ハンコの●の数)×4(ハンコを押した回数)」になるんだ。
つぎのことを覚えておいてね!
「3×4」
・「3」はハンコにある●の数
・「×4」は、ハンコを4回押したという意味
さて、「3×4」は九九で覚えたよね。
12だよね。
だから、●の数は「3×4=12」と計算できるんだ。
本当に12個あるか数えてみて。
実際はもっとていねいに教えていきますが、これでかけ算のイメージをつくります。ちなみに、九九を覚えさせるとき、布石として「3×□=12」などの問題を自作して、九九を強化します(後述の割り算に話がつながります)。そういう話もすべて割愛しています。
かけ算のイメージがあれば、面積図もかんたん!
「3×4」
さっきはハンコだったけど、●を描くの、面倒だよね。
ハンコの●の数は3つ。ハンコの●はたてに並んでいたよね。だから、たては3。
ハンコをよこに4回押していくんだよね。だから、よこは4。
というわけで、「3×4」は、つぎようにするね。
「?」はいくつ?

「3×4=12」だよね。
ものすごく些細なところですが…。面積の公式「たて×よこ」を教えていません。「かけ算のハンコ」から「面積」を教えているので、四角形の面積の公式を教えなくてもいいわけですね。
割り算は分割法からイメージさせる
※割り算は単位あたりを教えると効率的ですが、消化不良になるので最初は教えません(子どもが苦手とする単位を先にしっかりと教えて、かつ、その意味も理解させないといけないわけですからね)。一番理解しやすい、かつ、今後の布石になる分割法を軽く教えるだけに、とどめています。
●が12個並んでいるよね。
これを4人に等しく分けるにはどうすればいい?

つぎのようにすればいいよね。

12を等しく4人に分けるとき、「12÷4」と書くんだ。
「÷4」は「4で等しく分ける」という意味だから覚えておいて。
これを四角の図にできる?
●はぜんぶで12個あるわけだよね。
それを4つに等しく分けたわけだから、つぎのような図になるよね。
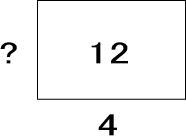
割り算(分割法)というルールが加わりました。
かけ算と割り算の関係性から、わり算の計算方法をイメージさせる
「18÷3」はいくつ?
●が18個あるとするね。
それを「÷3」にしたんだよね。
「÷3」はどういう意味だった?
そうだよね。「等しく3つに分ける」という意味だったよね。
18を「3つに等しく分ける」わけだから、図にすると、以下になるね。
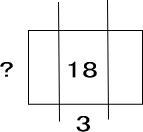
わからない?
●にしてみるね。
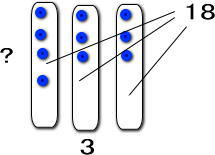
「?」って、3をかけたら18にな数じゃない?
「?×3=18」
だから、6だよね。
「かけ算はハンコ」「割り算は等しく分ける」という2つのルールから、割り算の計算法をイメージできるようになりました。
実際はもっとていねいに解説して、練習問題も解かせます。
で、最初の布石はここで回収します。つまり、「3×□=18」の計算を鍛えているから、ここはすんなり進めるわけです。
ちなみに、割り算だけ単位が変わりますが、ここを教えてしまうと、どツボにはまることがあるので(※)、さらっと進みます。
※数学が苦手な「中学生」でも理解できません(数学が苦手とはいえ、中学生ですからね)。ただし、優秀児だと、先に単位当たりから教えたほうが効率的だと思います。
たった2つのイメージで、逆数ができる!(小4の受験算数)
※前提として、すでに分数を教えていて「3÷8」のような練習問題を解いているとします。
「5×□=3」の□はいくつ?
わからない?
かけ算は、面積図で表せたじゃん。
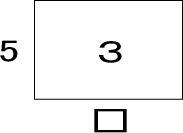
「5にいくつをかければ3になるかわからない」って?
ぐるりと、まわしてみよう!
こうすれば見たことがある図にならない?
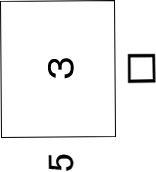
わり算だよね。
3を等しく5で分けた図だよね。
「等しく5で分けた」は「÷5」だから、「3÷5=5分の3」になるんだ。
中学では「右辺と左辺を等しい数字で割る」という公式のようなものを覚えさせられます。しかし、前述の通り、かけ算と割り算のルールがわかっていれば、これを覚えなくてもできます。
ちなみに、「アレイ図は〜」「かけ算の順序が〜」などと言い出すかたは、そっとこのページを閉じてください 笑
割り算の余りの処理(小4の受験算数)
※包括法ですが、低年齢なので消化不良を避けるために、強引に分割法で教えました。
「51人がいて、4人掛けのイスがある。いくつイスは必要?」
わからないって?
想像してみて。
ここに51人いて、向こうにイスがあったとするね。
51人のうち、まずは、4人がイスに座りに行ったんだよ。
つぎに、別の4人がイスに座ったんだよ。
これを図にするね。
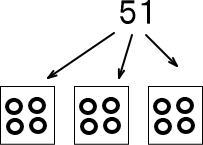
51人を4人ずつ等しく分けてない?
そう。
割り算だよね。
だから、51÷4にするんだ。
でも、計算すると「51÷4=12・・3」と余りがでてしまう。
これ、どういう意味?
12の意味はわかるよね。
4人のまとまりが、12個できたってことだから、イスは12きゃくってこと。(←さらっと書いていますが、割り算の文章題で鍛えておく必要があります)。
つぎに、余りの3はどういう意味?
図のように、4人ずつ座っていったら、3人座れなかったってことだよね。
というわけで、答えはいくつ?
12きゃくって?
それじゃ、余った3人座れないじゃん 笑
その3人も座るから、答えは13きゃく。
つぎの周期算のために、かなり端折った解説になりました。実際はいろいろと鍛えてから、この余りの話になります。
ちなみに、ここでもイメージで教えていることがわかると思います。
周期算(小4の受験算数)
51番目の碁石は何色?
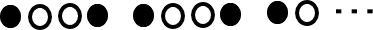
51番目まで、碁石があるんだよね。
これは碁石が51個あるってことだよね。
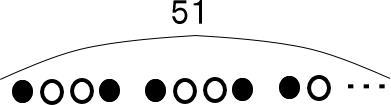
よく見てみて、「●○○●」が同じだよね!
ここで、4つの碁石を袋にいれるね。
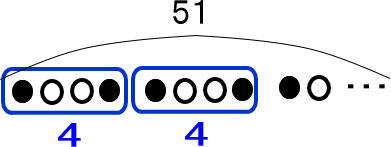
あれ?
どこかで見た図じゃない?
イスの問題と同じだよね!

51が4つのカタマリで(袋)、分けられているんじゃない?
袋の数を計算すると「51÷4=12・・・3」だよね。
12は何の数?
そう。
袋の数。
じゃあ、3は?
そう。
碁石が3つ余ったってことだよね。
答えはもうわかるよね。
51番目の碁石は、3つ余ったところの3つ目だから「〇」だよね!
かなり端折った解説ですが、周期算は、かけ算とわり算がしっかり理解できていれば解けるとわかっていただけたのではないでしょうか。
「●番目と▲番目の真ん中は何番目?」
「8番目と32番目の真ん中は何番目?」のような計算がありますよね。
「足して2で割る」と覚えさせれば済みますが、わたしはモノ(おはじき)を使って、2通りの計算方法を教えます。
※順番は「下記1→下記2」です。
1.基数と序数を意識させる計算方法
2.実践的な計算方法
なぜ2つの計算方法を教えるのでしょうか。
理由は2つあります。
1つ目。
上記1は、基数と序数を教えたあと、子どもに基数と序数を意識させるのに、ちょうど良いからです。
2つ目。
上記2は、算数の思考力が育っていない子どもには、わかりにくいためです。だから、まずは上記1から、というわけです(ふつうは小3で学ぶので、いきなり上記2でも大丈夫でしょうが、うちは年長にも教えています)。
つまり、わたしは、子どもの算数の思考力にあわせて、教えたかを変えています。もっというなら、算数の思考力が育っていないときは基数と序数の練習として上記1、それなりに育ったあとは上記2で実践的な計算方法を教えています。
というわけで、ここでは2つの教えかたが、どのようにちがうのかを紹介します!
基数と序数を意識させる計算方法
まずは、基数と序数のときの教えかたです。
こちらのほうが理解しやすいのですが、計算が遅くなります。
真ん中とは?
7つの●があったとするね。
真ん中に色をぬってみて。

そうだよね。
つぎのようになるよね。

ほら、見て。
真ん中より左と右、同じ数になるよね。
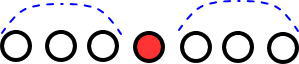
じゃあ、真ん中よりも左(右)に●がいくつあるか計算してみよう!
計算しなくても「3」だとわかるって?
今は図を見ればわかるけど、たとえば「1241243」の真ん中よりも左(右)の●の数、わかる?
●を1241243個、描いて、数えるの?
できないよね 笑
というわけで、計算していくね。
まずは、真ん中の●にはいなくなってもらうね!
さようなら!
式でいえば、7個から真ん中の1個がなくなるから、「7−1」だよね。
残りは6。

真ん中だから右と左は同じ数になるよね。
残った「6」を半分にして「6÷2=3」。
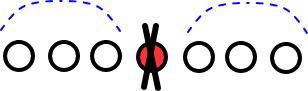
よって、図のようになるよね!
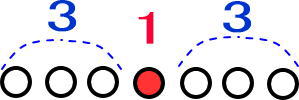
この後は数字を大きくして練習させるといいですよ。
出題するときは、奇数にしてくださいね。
(例)29の真ん中よりも左の●はいくつある?
<解説と解答>
29−1=28
・28÷2=14
・「14、1、14」と並んでいる(ここが重要)
1番目から●番目の真ん中
1番目から9番目の真ん中は何番だと思う?
わからないって?
まずは、「番目」を「人数」にするんだったね。
9番目まで、何人いる?
そうだね。
9人だね。
9人の真ん中を計算すればいいんだ。
これはさっき勉強したよね。
まずは、真ん中のひとにはいなくなってもらいます!
さようならー
すると「9−1=8」。
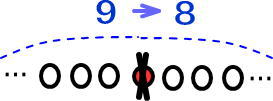
真ん中より左と右は等しくなるんだよね。
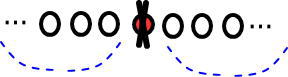
だから「8÷2=4」。
図のようになるよね。
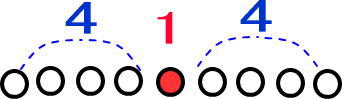
「4、1、4」と並んでいるから、真ん中は「4+1=5」。
5番目だね!
先ほどと同じなので、かんたんではないでしょうか。
●番目から▲番目の真ん中(流れを説明)
4番目から8番目のちょうど真ん中は何番目?
わからないって?
難しいよねー
まずは、図にしてみるね。

図をよく見て。
真ん中を計算するときに邪魔なやつらがいない?
1番目、2番目、3番目のやつ、邪魔だよねー
いなくなってもらいまーす!

いなくなったひとたちは、数字にします!
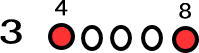
残ったひとは5人だよね。
これで、見たことがある図になったよね(前述の1番目から●番目の図のこと)。
この5人の真ん中を考えればいいんだ。
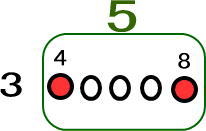
これはすでに勉強したよね。
1.真ん中のひとを消す! → 5−1=4
2.真ん中より左と右は等しいので2で割る! → 4÷2=2
だから、つぎのようになるよね。
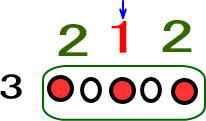
よって、「3+2+1」で、6番目が答え!
以下を覚えておいてね!
1.まずは邪魔者を消す!
2.残ったひとたちで真ん中を考える!
●番目から▲番目の真ん中(計算方法を説明)
さっきの問題、図を見ると3人いなくなるとか5人が残るとかわかるんだけど、たとえば「123番目から233番目の真ん中は何番目?」とか言われたら、図にできないよね。
だから、計算方法を教えるね。
(問)8番目から32番目の真ん中は何番目?
計算するときは、「番目」を「人数」にするんだったね。
1.まずは邪魔者を消す!
8番目の前の7人が邪魔だよね。
この7人にはいなくなってもらいます!
そして数字にするんだったよね。
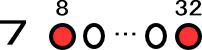
じゃあ、残りは何人いると思う?
「32−8」で計算すればいいと思う?
そうしてしまうと、8番目のひともいなくなっちゃうじゃん!
ダメだよねー
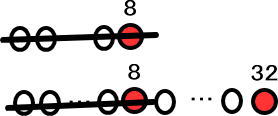
だから「32人から8人どっかにいけー」としたあと、「あ、8番目のひとだけ戻ってきて!」とすればいいんだ。つまり1を足せばいいよね。
「32−8+1」で、25人。
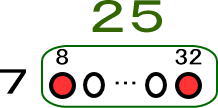
あとは、25人の真ん中を考えるんだったよね!
1.真ん中のひと、どこかにいってもらいます! → 25−1=24
2.真ん中より左と右は等しいので2で割る! → 24÷2=12
だから、つぎの図のようになるよね。
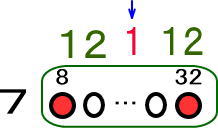
よって、答えは「7+12+1」で、20番目。
実践的な計算方法
「●番目と▲番目の真ん中は何番目?」は、(●+▲)÷2で一発で計算できますが、なぜそのように計算できるのかを説明しておくと忘れにくくなります。
なぜそのように計算できるのかの教えかたです。
ちなみに、こちらは、理解しにくいのですが、計算がはやくなります。
真ん中は何個目?
7つの●があったとするね。
真ん中に色をぬってみて。

そうだよね。
つぎのようになるよね。

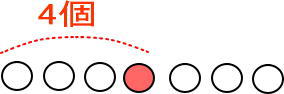
左から真ん中まで数えてみて。
4個あるよね。
真ん中は左から数えて4個目だよね。
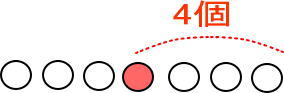
右から真ん中まで数えてみて。
4個あるよね。
真ん中は右から数えて4個目だよね。
真ん中の数は左から数えても、右から数えても同じだって覚えておいて!
真ん中まで同じ個数を利用
3番目と9番目の真ん中は何番目か考えてみよう!
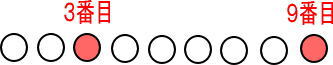
真ん中ってことは、3番目から数えても、9番目から数えても同じなんだよね。
まずは、3番目から数えていく場合ね。
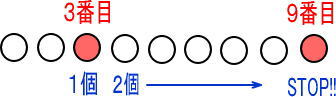
つぎに、9番目から数えていく場合ね。
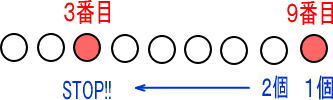
これが同じになるんだよね。
どうやって考えればいいと思う?
おはじきを使って考えてみよう!
わかった?
わからないって?
一緒に考えていこう!
まとめると、このようになるよね。
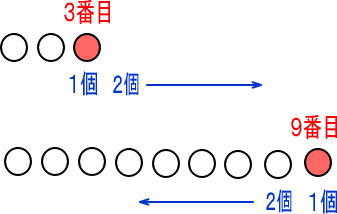
よく見て。
今回の話って、赤い四角のなかだけの話だよね。
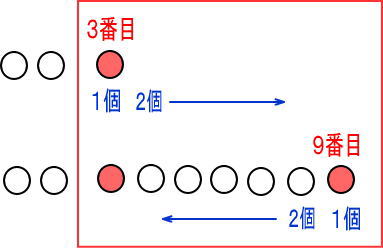
コレ、何がややこしいのかっていうと、9番目が逆から数えないといけないってところ。
だから、チョキチョキ切りとって、ひっくり返すね。
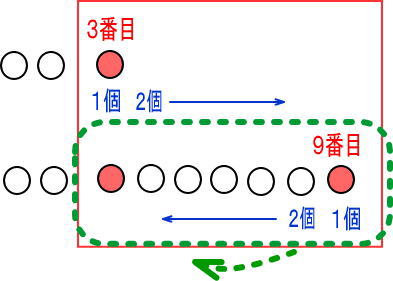
ひっくり返すと、つぎのようになるよね。
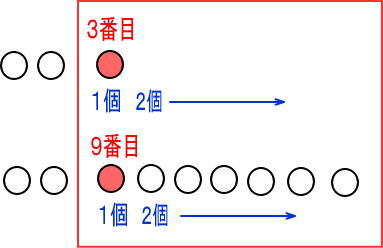
え?
ひっくり返してもいいのかって?
9番目から真ん中まで何個あるのかを数えるだけだから大丈夫だよね!
…納得できないって?
じゃあ、つぎの図を見て。
右から数えているよね。

これをひっくり返しても4個目は4個目だよね。
同じだよね?
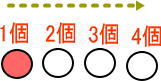
納得できた?
じゃあ、話を元に戻すね。
つぎの図だったね。

これでわかるよね。
3個移動させれば同じになるね!
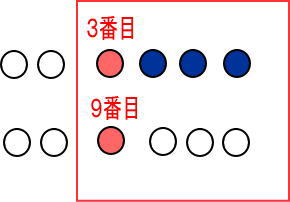
だから、3番目と9番目の真ん中は6番目なんだ。
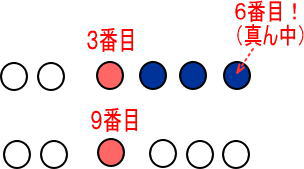
9番目のほうから考えても、やはり6番目だね!

ややこしいので、おはじきでも使って子どもに実際にさせるようにしましょう!
実践的な計算方法を教える!
さっきの話をまとめると以下ね。
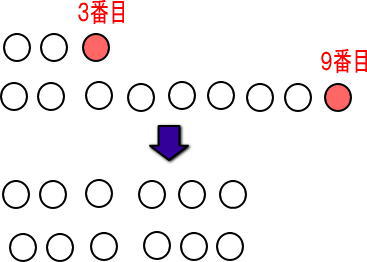
これ、どこかで見たことがあるよね。
そう。
平均だよね。
だから「(3+9)÷2=6」で、6番目と一発で計算できるんだ!
最初からそれを教えろって? 笑
なぜか理由がわからないとすぐに忘れるから、しっかり勉強したんだよ!
困ったプロも多い!
教えかたのサンプルを見ていただければわかっていただけたと思いますが、わたしは公式をほとんど使いません。
それは、今回の場合だと「かけ算のハンコ」「わり算のイメージ」「あまりのイメージ(今回は割愛しました)」という根本がわかっていれば、逆算や周期算などは、教えなくても解けるためです(公式なんて教える必要はない! もっとも、はやく解くために最終的には覚えさせます)。
また、かけ算やわり算を深く理解するための逆算や周期算なので、受験算数こそ、算数の思考力を育てるためのツールだと、わたしは考えています。
「単に難問を解かせているだけなのに深く理解させている」「公式を根本」などと主張するプロもいて、挙句に「受験算数は思考力を奪う」なんていう、とんでもないことまでいうかたたちもいて、閉口しています。